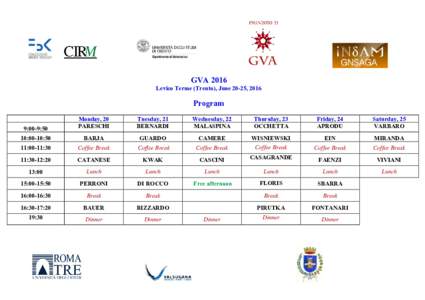
<--- Back to Details
| First Page | Document Content | |
|---|---|---|
 Date: 2010-09-12 06:06:46Geometry Algebraic geometry Algebra Algebraic varieties Projective geometry Fano variety Birational geometry Projective variety Fano Olivier Debarre Ample line bundle |
Add to Reading List |
 Fano threefolds The nodal Fano threefold X10 Reconstructing X10 Verra threefolds Period maps
Fano threefolds The nodal Fano threefold X10 Reconstructing X10 Verra threefolds Period maps